In Teil 2 wurden wir von der DIVI an das RKI verwiesen und freundlicherweise wurde uns der RKI-Wochenbericht vom 2. Dezember gleich mitgeliefert. Schauen wir uns also mal an, was sich daraus bezüglich des Impfstatus der hierzulande an Covid-19 Erkrankten ergibt:
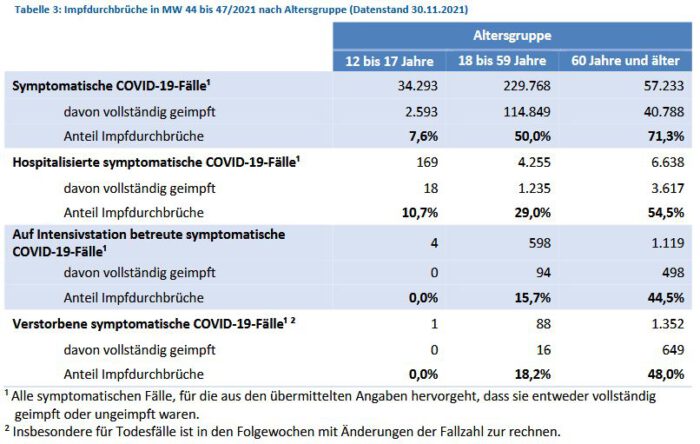
Zu den Zahlen gibt es noch diese Info:
Den letzten Satz überliest man leicht, aber er ist wichtig, denn er weist darauf hin, dass es auch hier eine Dunkelziffer gibt von Fällen, deren Impfstatus nicht bekannt ist. Wenn diese Dunkelziffer wie im Beispiel zuvor in etwa der Zahl der Fälle mit bekanntem Impfstatus entspricht, dann sind diese Zahlen genauso unbrauchbar wie Söders Inzidenzen. Leider ist die Dunkelziffer in der Tabelle zu den Impfdurchbrüchen nicht angegeben – warum wohl…?
Ein Hinweis auf die Dunkelziffer findet sich auf Seite 15 des Lageberichts:
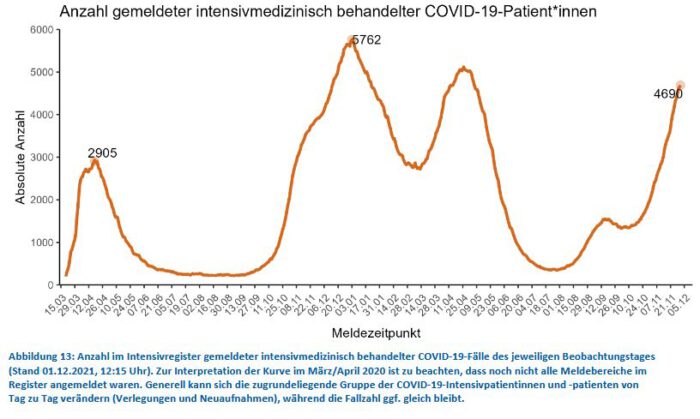
Demnach waren Anfang Dezember 4690 Personen auf Intensivstationen.
Wenn man die entsprechenden Werte der Altersgruppen in Tabelle 3 zusammenrechnet, kommt man auf bescheidene 1721 Intensivpatienten, also eine sehr große Differenz zur oben angeführten Zahl von 4690 Patienten. Allerdings bezieht sich Tabelle 3 auf den Zeitraum 1.11. bis 28.11. und nicht auf den Wert von Anfang Dezember. Nimmt man einen gleichmäßigen Anstieg im Verlauf des November an, müssten zur Mitte des genannten Vierwochenzeitraums etwa 3250 Patienten auf Intensivstationen gelegen haben. Das ist fast doppelt so viel wie die nach Alter und Impfstatus aufgeschlüsselte Summe von 1721 Intensivpatienten. Das RKI hat also das gleiche Problem wie Söder und sein LGL: Die Zahlen sind aufgrund der hohen Dunkelziffer wenig bis gar nicht aussagefähig. Darauf müsste das RKI explizit hinweisen, anstatt die Dunkelziffer im Kapitel über die Impfdurchbrüche einfach zu unterschlagen.
Begründung: Warum sind die RKI-Zahlen wenig aussagekräftig?
Wenn wir wie vorher vorgehen und die Dunkelziffer einbeziehen, kommen wir auf folgende Werte für die Intensivpatienten:
Geimpft + ungeimpft: 4 + 598 + 1119 = 1721 Patienten
Vollständig geimpft: 94 + 498 = 592 Patienten
=> Nicht geimpft: 1721-592 = 1129 Patienten
Gesamt: Ca. 3250 Patienten
=> Impfstatus unbekannt: 3250 – 1721 = 1529 Patienten
Um die Schwankungsbreite der Impfdurchbrüche bei Berücksichtigung der Dunkelziffer zu berechnen, wenden wir zunächst die “Methode Söder” an: Die Dunkelziffer wird den Ungeimpften zugeschlagen.
(1129 + 1529) / 3250 = 81,8 ungeimpfte Patienten
592 / 3250 = 18,2 % geimpfte Patienten
Was passiert, wenn man die Unbekannten stattdessen den Geimpften zurechnet? Die Mehrzahl der Deutschen ist geimpft, also ist diese Version eigentlich die naheliegendere:
1129 / 3250 = 34,7 ungeimpfte Patienten
(592 + 1529) / 3250 = 65,3 geimpfte Patienten
Für die Impfdurchbrüche ergibt sich so eine Schwankungsbreite zwischen 18,2 und 65,3 Prozent. Letzteres entspricht beinahe der Zahl der Geimpften in der Gesamtbevölkerung!
Immerhin geht das RKI nicht (mehr) nach der “Methode Söder” hin und rechnet die Unbekannten einfach zu den Ungeimpften dazu. Das war offenbar nicht immer so:
https://correctiv.org/faktencheck/2021/11/19/das-rki-stufte-menschen-mit-unbekanntem-impfstatus-als-ungeimpft-ein-das-hat-schaetzung-zur-impfeffektivitaet-leicht-beeinflusst/
Auf Basis der Impfdurchbrüche kann man die Wirksamkeit der Impfung berechnen, wenn man die Impfquote kennt. Logischerweise ist die Wirksamkeit Null, wenn die Impfquote gleich der Quote der Impfdurchbrüche ist.
Das RKI verwendet dafür die Farrington-Formel:
Mit…
VE = Impfeffektivität
PCV = Anteil der Geimpften an den (schwer) Erkrankten (Impfdurchbrüche)
PPV = Anteil der Geimpften an der untersuchten Grundgesamtheit (Impfquote)
…lautet die Formel:
VE = 1 – PCV/(1- PCV) * (1-PPV)/PPV
Es ist klar, dass aufgrund der hohen Schwankungsbreite bei den Impfdurchbrüchen – je nachdem, welcher Seite man die Dunkelziffer zurechnet – auch für die Wirksamkeit nur Blödsinn rauskommen kann. Spaßeshalber mache ich die Rechnung trotzdem, ausgehend von einer Impfquote von 67 % (gemäß dem Stand im Betrachtungszeitraum, also Mitte November).
VE = Impfeffektivität
PCV = 18,2 %
PPV = 67 %
VE = 1 – 0,182/(1- 0,182) * (1-0,67)/0,67 = 1- 0,182/0,818 * 0,33/0,67 = 1 – 0,222 * 0,493
= 1- 0,109 = 0,891 = 89 %
Jetzt das andere Extrem:
PCV = 65,3 %
PPV = 67 %
VE = 1 – 0,653/(1- 0,653) * (1-0,67)/0,67 = 1- 0,653/0,347 * 0,33/0,67 = 1 – 1,882 * 0,493
= 1- 0,928 = 0,072 = 7 %
Wie gesagt, diese Rechnung ist Blödsinn, Ein Ergebnis, das zwischen 7 % und 89 % schwankt, ist gleichbedeutend mit gar keinem Ergebnis.
Das RKI macht diese Rechnung trotzdem, indem es die Dunkelziffer einfach unterschlägt. Man kommt so auf recht ordentliche Ergebnisse mit einer Impfwirkung bezüglich schwerster Erkrankung von weit über 80 Prozent:
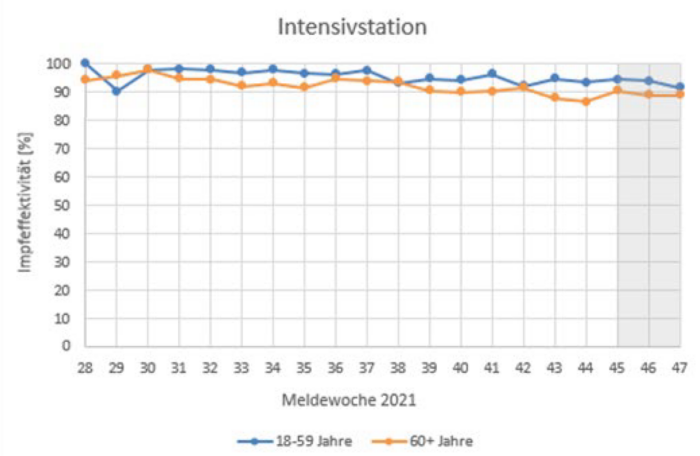
Da die Patienten mit unbekanntem Impfstatus aber nicht weg sind, sondern entweder geimpft oder ungeimpft, also zu gewissen Teilen der einen und der anderen Gruppe zugerechnet werden müssen, und vor allem, weil sie so viele sind, ist diese Unterschlagung eine recht willkürliche Beeinflussung des Ergebnisses. Das RKI müsste das erwähnen und den Bereich der Unsicherheit seiner Berechnung mit angeben. Es tut dies aber nicht – ein Schelm, wer Böses dabei denkt!
Ein halbwegs plausibler alternativer Ansatz anstelle der Unterschlagung der Dunkelziffer wäre, wenn man die 1529 Patienten mit unbekanntem Impfstatus entsprechend der bundesweiten Impfquote von etwa 67 % aufteilt, also 0,67 * 1529 = 1024 Personen den Geimpften zurechnet und entsprechend 505 den Ungeimpften.
(1129 + 505) / 3250 = 50,3 % ungeimpfte Patienten
(592 + 1024) / 3250 = 49,7 % geimpfte Patienten
Für die Wirksamkeit ergibt sich damit:
VE = Impfeffektivität;
PCV = 49,7 %
PPV = 67 %
VE = 1 – 0,497/(1- 0,497) * (1-0,67)/0,67 = 1- 0,497/0,503 * 0,33/0,67 = 1 – 0,988 * 0,493
= 1- 0,487 = 0,513 = 51 %
51 % Impfwirksamkeit, jede zweite Impfung wäre demnach ein Versager. Das passt immerhin zur aktuell im Vergleich zum Vorjahr ähnlich hohen Intensivbelegung. Mit einer “Pandemie der Ungeimpften” lässt sich diese nämlich nicht erklären, wenn in der Hauptrisikogruppe der über Sechzigjähtigen nur ein Bruchteil von etwa 15 % nicht geimpft ist.
Fazit: Auch bei den RKI-Zahlen zum Impfstatus ist die Dunkelziffer so hoch, dass sich daraus keine seriösen Aussagen ableiten lassen. Insbesondere lässt sich damit keine Impfeffektivität berechnen, wenn deren Schwankungsbreite zwischen 7 und 89 Prozent liegt.
Die mit einer solchen Wirksamkeit begründete berufsbezogene Impfpflicht ist Ausdruck und Folge einer “Tyrannei der Unwissenden”.
Anmerkung: Die Farrington-Formel und die Abschätzung der 3250 habe ich von hier: https://norberthaering.de/news/rki-farrington/
Nachtrag 21.12.2021: Einer, der sich mit Statistik auskennt, zieht ein ähnliches Fazit:
Es ist gezeigt worden, dass die Datenlage mangelhaft ist sowohl hinsichtlich der Qualität als auch der Quantität, dass die Impfquote unsicher ist und von der Methode der Berechnung systematisch überschätzt wird und dass wichtige Größen völlig unbekannt sind und nicht in die Berechnung eingehen. Die Berechnungen sind nicht falsch, aber sie enthalten so viele Unsicherheiten, dass man diese Kennzahlen nicht als verlässliche Basis für weitreichende politische Entscheidungen ansehen kann.
https://politicaldatascience.blogspot.com/2021/12/deep-dive-impfeffektivitat-eine.html?m=1
OxHVIdjyYqQWnB
TVGRdEHPWlpv